CipherLore

& Bitwise Operators

Bitwise operators work on individual bits within a number. Unlike arithmetic operators that treat numbers as mathematical values, bitwise operators treat them as sequences of independent bits — each position processed separately.

↻ Shifts & Rotations

± Two's Complement

How do computers represent negative numbers? The naive approach would be to reserve one bit as a "sign bit" — 0 for positive, 1 for negative. But this creates problems: you'd have both +0 and -0, and addition would require special logic to handle signs.

Two's complement is a more elegant solution that's been universal since the 1960s. The rule is simple: to negate a number, flip all the bits and add 1. This single rule produces a number system where:

• There's only one zero (no +0/-0 confusion)
• Addition works identically for signed and unsigned numbers
• The hardware doesn't need to know which you're using
• Subtraction is just addition of the negated value

Let's see why this works. Take the 8-bit number +1: 00000001. To negate it, flip all bits: 11111110. Then add 1: 11111111. That's -1 in two's complement.

Now try adding them: 00000001 + 11111111 = 100000000. That's 9 bits — but we only have 8, so the top bit overflows and is discarded, leaving 00000000. We get zero, exactly as expected from 1 + (-1). The math just works, with no special cases.

The sign bit is the highest bit. If it's 1, the number is negative. For 8-bit: values 0-127 are positive, 128-255 represent -128 to -1. For 32-bit: the cutoff is at 2³¹ (about 2.1 billion). This is why 0xFFFFFFFF (all 32 bits on) equals -1 when interpreted as signed, not 4 billion.

Programming languages each handle this differently. Cryptographic algorithms are specified mathematically — "add these 32-bit unsigned integers" — but languages have their own ideas about how numbers work. Some languages, like JavaScript, have quirks where bitwise operations might treat numbers as signed, requiring special idioms to force an unsigned interpretation. Other languages, like Python, have arbitrary precision integers that never overflow, necessitating explicit masking to simulate fixed-width behavior. Languages like Go and Rust offer explicit sized types (e.g., uint32, i64) that more closely align with cryptographic specifications.

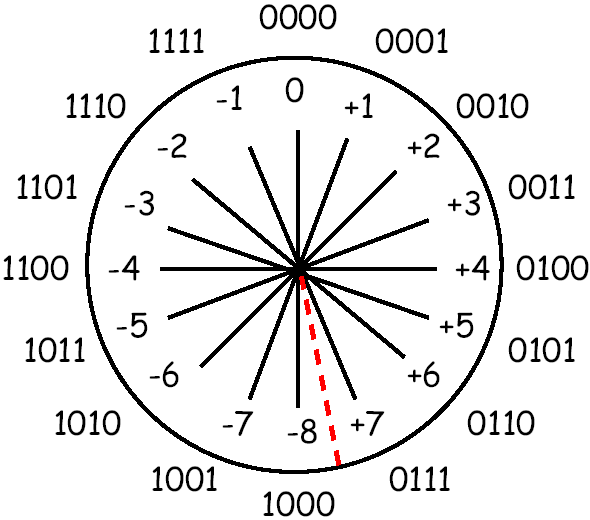
4-bit two's complement shown as a clock. Adding 1 moves clockwise; subtracting moves counter-clockwise. The red line marks where positive (+7) wraps to negative (-8).

🏆 Challenges

🔒 All Ones Find −1 in binary

🔒 Overflow! Make 127 overflow to −128

🔒 DIY Negate Negate a number using NOT then +1

🔒 Underflow! Make negative − 1 = positive

🗂 Non-Cryptographic Hashing

Use Cases

• Hash tables: Convert a key (like a username) into an array index. "alice" → 7, "bob" → 3. Fast O(1) lookups. The function just needs to distribute keys evenly — security doesn't matter.
• Checksums: Add up all bytes in a file (mod some number). Detects accidental corruption like bit flips during transmission. Trivial to bypass intentionally.
• CRC (Cyclic Redundancy Check): Polynomial division over binary data. Better at catching burst errors than simple checksums. Used in Ethernet, ZIP files, PNG. Still not secure — you can craft files with any CRC you want.

An attacker can easily find collisions or craft inputs with specific hash values. For hash tables, that's fine — for passwords, it's catastrophic.

Classic Algorithms

Here are the hash functions you'll encounter in real codebases:

DJB2 (Dan Bernstein, 1991)

The most famous hash table hash. Used in glibc, Perl, Python 2, and countless projects:

function djb2(str) {
    let hash = 5381;              // Magic starting value
    for (let i = 0; i < str.length; i++) {
        // hash * 33 + char  (33 = 2^5 + 1, fast to compute)
        hash = ((hash << 5) + hash) + str.charCodeAt(i);
        hash = hash >>> 0;        // Keep as 32-bit unsigned
    }
    return hash;
}
// djb2("hello") → 261238937

Why 5381? Why 33? Bernstein found these empirically — they give good distribution. That's the key difference from crypto: constants are chosen for speed and spread, not to resist mathematical attacks.

FNV-1a (Fowler-Noll-Vo)

Used in DNS, game engines, and many hash tables. The "1a" variant XORs before multiplying:

function fnv1a(str) {
    let hash = 2166136261;        // FNV offset basis
    for (let i = 0; i < str.length; i++) {
        hash ^= str.charCodeAt(i);
        hash = Math.imul(hash, 16777619);  // FNV prime
        hash = hash >>> 0;
    }
    return hash;
}
// fnv1a("hello") → 1335831723

The magic numbers (offset basis and prime) are chosen so similar inputs produce different outputs — but there's no cryptographic analysis, just empirical testing.

Java's String.hashCode()

Polynomial hash, simple but effective:

function javaHash(str) {
    let hash = 0;
    for (let i = 0; i < str.length; i++) {
        hash = ((hash << 5) - hash) + str.charCodeAt(i);  // hash * 31 + char
        hash = hash | 0;          // Convert to 32-bit signed int
    }
    return hash;
}
// javaHash("hello") → 99162322

Modern Fast Hashes

For applications needing high throughput (hash tables with billions of entries, network packet processing), modern alternatives include:

• xxHash: Extremely fast (GB/s speeds), good distribution. Used in databases and compression tools.
• MurmurHash: Fast, well-distributed. Popular in distributed systems and databases.
• SipHash: A middle ground — fast but with some security properties. Used in hash tables to prevent DoS attacks via hash flooding.

# Cryptographic Hashing

Security Properties

Cryptographic hash functions add three security properties that non-cryptographic hashes lack:

• Preimage resistance: Given a hash output, you can't find any input that produces it (can't reverse the hash).
• Second preimage resistance: Given one input, you can't find a different input with the same hash (can't forge a document).
• Collision resistance: You can't find any two different inputs with the same hash (even if you choose both).

Hash functions are one-way: given the output, there's no mathematical formula to recover the input. This isn't encryption (which is reversible by design) — it's closer to scrambling an egg. The only way to "reverse" a hash is to guess inputs until you find one that produces the target output (a brute-force attack). For SHA-256, this would take longer than the age of the universe.

The avalanche effect ensures that changing even a single bit of input changes approximately 50% of the output bits, in an unpredictable pattern. This makes it impossible to work backwards: similar inputs don't produce similar outputs, so you can't "get warmer" when guessing.

Hashes are everywhere: storing passwords (you store the hash, not the password), verifying file integrity (download matches expected hash?), digital signatures (sign the hash, not the whole document), blockchain (each block contains the hash of the previous block), and content-addressable storage (the hash IS the address).

Performance: Hash functions process data in fixed-size blocks (512 bits for SHA-256). The time to hash grows linearly with input size — hashing 1MB takes roughly 1000× longer than hashing 1KB. But "longer" is relative: modern CPUs with dedicated SHA instructions can hash gigabytes per second. The widget below demonstrates this — try typing increasingly long strings and notice the hash updates instantly.

Hash Function Genealogy

⚙ SHA-256 Internals

Step 1: Pad the Message

SHA-256 processes data in 512-bit (64-byte) blocks. Your message is padded to fit: add a 1 bit, then zeros, then the original message length as a 64-bit number. This ensures every message has a unique padded form.

Step 2: Initialize Eight Registers

The hash state is eight 32-bit numbers (a–h), initialized to the fractional parts of the square roots of the first 8 primes. These "nothing up my sleeve" numbers prove no backdoor was inserted — anyone can verify that 0x6a09e667 = frac(√2) × 2³².

Step 3: Expand 16 Words → 64 Words

Each 512-bit block is split into 16 words (32 bits each). These are expanded to 64 words using a mixing function: each new word combines earlier words with rotations and XORs. This spreads the influence of each input bit across more rounds.

Step 4: Run 64 Rounds

This is the heart of SHA-256. Each round:

• Mix the bits: Rotate and XOR registers to create two temporary values
• Add the message: Combine with the current word and a round constant (cube roots of primes)
• Shift the registers: Each register moves down (h←g←f←...←b←a), while new values enter at 'a' and 'e'

After 64 rounds, every input bit has influenced every output bit — this is the avalanche effect in action.

Step 5: Add to Initial Values

The final register values are added to the initial values (mod 2³²). This addition is crucial — it makes the compression function one-way. Without it, you could reverse the rounds.

One Round Visualized

Click in the code to highlight the corresponding diagram element:

1 A–H: Eight 32-bit registers (hash state)

2 Ch: "Choose" — E selects bits from F or G

3 Σ1: Rotate & XOR to mix bits of E

4 Ma: "Majority" — outputs majority of A,B,C

5 Σ0: Rotate & XOR to mix bits of A

6 W_t: Message word for this round

7 K_t: Round constant (cube roots of primes)

8 ⊞ Addition mod 2³² (red boxes)

One round of SHA-256 compression. Source: Wikipedia

JavaScript Python Go Rust

JavaScript — Full SHA-256 Implementation Run ▶

Right rotation explained

>>> vs >>: >>> is unsigned right shift (fills with 0s). >> preserves the sign bit. Crypto needs unsigned.

Why 32-n? To rotate right by n bits: shift right n (bits fall off right), OR with shift left 32-n (puts those bits on the left). It's a circular shift on 32-bit integers.

Bit rotation explained

>>> is unsigned right shift (fills with 0s). >> would preserve the sign bit — wrong for raw bits. << is left shift. Why 32-n? In a 32-bit rotate, bits that "fall off" the right must wrap to the left. x>>>n keeps the high bits; x<<(32-n) moves the low n bits to the top. OR combines them.

Why pad with length?

Without the length, "abc" and "abc\0\0\0..." would hash the same after padding. The 64-bit length also prevents length extension attacks — you can't append data without knowing the original length.

"Nothing up my sleeve" numbers

Why primes? Primes have no hidden structure — they can't be factored, so there's no "trick" to exploit. Why roots? √ and ∛ produce irrational numbers whose digits look random but are reproducible. Anyone can verify H0 = frac(√2)×2³² = 0x6a09e667. If the NSA had just picked hex values, you'd have to trust them.

Why √ for H and ∛ for K?

Using different operations (square vs cube root) ensures H and K are mathematically independent. If both used √, there might be some algebraic relationship an attacker could exploit. The primes are also different: H uses primes 2-19, K uses primes 2-311.

Why expand 16 words to 64?

The message schedule mixes earlier words into later rounds. The mixing functions (s0/s1 in code) use different rotation amounts to ensure each input bit affects many output bits — creating the avalanche effect.

Why these specific functions?

Ch: "if x then y else z" — non-linear selection. Maj: "majority vote" — also non-linear. Combined with rotations, these resist linear and differential cryptanalysis.

Why 64 rounds?

Cryptanalysts found attacks on reduced-round SHA-256 (up to 46 rounds). 64 provides a safety margin. Each round mixes bits further — after 64, every output bit depends on every input bit.

// Complete SHA-256 implementation with explanations const message = "abc"; console.log("Message:", message, "\n"); // Right rotate: bits that fall off the right wrap to the left // @info:sha-rotr // >>> = unsigned right shift (fills with 0, not sign bit) // << = left shift (only one version exists) // Example: rotr(0b11001010, 3) = 0b01011001 const rotr = (x, n) => (x >>> n) | (x << (32 - n)); // === WHY PRIMES? WHY ROOTS? === // @info:sha-primes // The constants must look "random" but be verifiable (no hidden backdoors). // Primes have no hidden structure. Roots produce irrational decimals. // Anyone can verify: H0 = floor(frac(√2) × 2³²) = 0x6a09e667 const primes = [2, 3, 5, 7, 11, 13, 17, 19]; console.log("=== Deriving H from √primes ==="); const H = primes.map((p, i) => { const sqrt = Math.sqrt(p); // √2 = 1.41421356... const frac = sqrt - Math.floor(sqrt); // 0.41421356... const h = Math.floor(frac * 0x100000000); // × 2³² → 0x6a09e667 console.log(`H${i} = frac(√${p}) × 2³² = 0x${h.toString(16)}`); return h; }); // K uses CUBE roots (∛) of first 64 primes — different operation! // @info:sha-cube // Why different? So H and K are mathematically independent. console.log("\n=== K from ∛primes (first 4 of 64) ==="); const firstPrimes = [2, 3, 5, 7]; firstPrimes.forEach((p, i) => { const cbrt = Math.cbrt(p); const frac = cbrt - Math.floor(cbrt); const k = Math.floor(frac * 0x100000000); console.log(`K${i} = frac(∛${p}) × 2³² = 0x${k.toString(16)}`); }); // Full K array (precomputed for performance) const K = [ 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 ]; // STEP 1: Pad message to multiple of 512 bits // @info:sha-padding const msgBytes = new TextEncoder().encode(message); const bitLen = msgBytes.length * 8; const padBytes = new Uint8Array(64); // One 512-bit block padBytes.set(msgBytes); padBytes[msgBytes.length] = 0x80; // Append '1' bit new DataView(padBytes.buffer).setUint32(60, bitLen, false); // Append length console.log("Padded block (hex):", Array.from(padBytes).map(b=>b.toString(16).padStart(2,'0')).join('')); // STEP 2: Parse into 16 32-bit words const W = new Uint32Array(64); const view = new DataView(padBytes.buffer); for (let i = 0; i < 16; i++) W[i] = view.getUint32(i * 4, false); // STEP 3: Extend to 64 words (message schedule) // @info:sha-schedule // s0(x) = rotr(x,7) ^ rotr(x,18) ^ (x>>>3) — mixes bits rightward // s1(x) = rotr(x,17) ^ rotr(x,19) ^ (x>>>10) — different rotations = different mixing for (let i = 16; i < 64; i++) { const s0 = rotr(W[i-15], 7) ^ rotr(W[i-15], 18) ^ (W[i-15] >>> 3); const s1 = rotr(W[i-2], 17) ^ rotr(W[i-2], 19) ^ (W[i-2] >>> 10); W[i] = (W[i-16] + s0 + W[i-7] + s1) >>> 0; } console.log("Message schedule W[0..3]:", Array.from(W.slice(0,4)).map(w=>w.toString(16))); // STEP 4: Initialize working variables let [a,b,c,d,e,f,g,h] = H; // STEP 5: 64 rounds of compression // @info:sha-functions // Ch(e,f,g) = (e AND f) XOR ((NOT e) AND g) — "choice": e chooses f or g // Maj(a,b,c) = (a AND b) XOR (a AND c) XOR (b AND c) — "majority" of 3 bits // Σ0(a) = rotr(a,2) ⊕ rotr(a,13) ⊕ rotr(a,22) — mixing for 'a' // Σ1(e) = rotr(e,6) ⊕ rotr(e,11) ⊕ rotr(e,25) — mixing for 'e' console.log("\nRound 0: a=" + a.toString(16) + " e=" + e.toString(16)); // @info:sha-rounds for (let i = 0; i < 64; i++) { const S1 = rotr(e, 6) ^ rotr(e, 11) ^ rotr(e, 25); const ch = (e & f) ^ (~e & g); const temp1 = (h + S1 + ch + K[i] + W[i]) >>> 0; const S0 = rotr(a, 2) ^ rotr(a, 13) ^ rotr(a, 22); const maj = (a & b) ^ (a & c) ^ (b & c); const temp2 = (S0 + maj) >>> 0; h = g; g = f; f = e; e = (d + temp1) >>> 0; d = c; c = b; b = a; a = (temp1 + temp2) >>> 0; if (i < 3) console.log(`Round ${i+1}: a=${a.toString(16)} e=${e.toString(16)}`); } console.log("... (rounds 4-63) ..."); // STEP 6: Add compressed chunk to hash const finalH = [(H[0]+a)>>>0,(H[1]+b)>>>0,(H[2]+c)>>>0,(H[3]+d)>>>0, (H[4]+e)>>>0,(H[5]+f)>>>0,(H[6]+g)>>>0,(H[7]+h)>>>0]; const ourHash = finalH.map(h => h.toString(16).padStart(8,'0')).join(''); console.log("\nOur SHA-256: ", ourHash); // Verify against Web Crypto const realHash = Array.from(new Uint8Array(await crypto.subtle.digest('SHA-256', msgBytes))) .map(b => b.toString(16).padStart(2, '0')).join(''); console.log("Web Crypto: ", realHash); console.log("Match:", ourHash === realHash ? "✓" : "✗");

Output

Python — SHA-256 Internals Exploration

import hashlib
import math

message = b"abc"
print(f"Message: {message.decode()}\n")

# === DERIVE H FROM √PRIMES ===
# Same formula the JavaScript version uses
primes = [2, 3, 5, 7, 11, 13, 17, 19]
print("=== H constants from √primes ===")
for i, p in enumerate(primes):
    sqrt = math.sqrt(p)
    frac = sqrt - int(sqrt)
    h = int(frac * 0x100000000)
    print(f"H{i} = frac(√{p}) × 2³² = 0x{h:08x}")

# === K FROM ∛PRIMES (first 4) ===
print("\n=== K constants from ∛primes ===")
for i, p in enumerate([2, 3, 5, 7]):
    cbrt = p ** (1/3)
    frac = cbrt - int(cbrt)
    k = int(frac * 0x100000000)
    print(f"K{i} = frac(∛{p}) × 2³² = 0x{k:08x}")

# === USE STANDARD LIBRARY ===
# Python's hashlib uses the same algorithm internally
result = hashlib.sha256(message).hexdigest()
print(f"\nSHA-256 (hashlib): {result}")

# Expected for "abc":
# ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad
print(f"Expected:          ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad")
print(f"Match: {'✓' if result == 'ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad' else '✗'}")

Go — SHA-256 Internals Exploration

package main

import (
    "crypto/sha256"
    "fmt"
    "math"
)

func main() {
    message := []byte("abc")
    fmt.Printf("Message: %s\n\n", message)

    // === DERIVE H FROM √PRIMES ===
    primes := []int{2, 3, 5, 7, 11, 13, 17, 19}
    fmt.Println("=== H constants from √primes ===")
    for i, p := range primes {
        sqrt := math.Sqrt(float64(p))
        frac := sqrt - math.Floor(sqrt)
        h := uint32(frac * 0x100000000)
        fmt.Printf("H%d = frac(√%d) × 2³² = 0x%08x\n", i, p, h)
    }

    // === K FROM ∛PRIMES (first 4) ===
    fmt.Println("\n=== K constants from ∛primes ===")
    for i, p := range []int{2, 3, 5, 7} {
        cbrt := math.Cbrt(float64(p))
        frac := cbrt - math.Floor(cbrt)
        k := uint32(frac * 0x100000000)
        fmt.Printf("K%d = frac(∛%d) × 2³² = 0x%08x\n", i, p, k)
    }

    // === USE STANDARD LIBRARY ===
    hash := sha256.Sum256(message)
    fmt.Printf("\nSHA-256 (crypto/sha256): %x\n", hash)

    expected := "ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad"
    fmt.Printf("Expected:                %s\n", expected)
    fmt.Printf("Match: %s\n", map[bool]string{true: "✓", false: "✗"}[fmt.Sprintf("%x", hash) == expected])
}

Rust — SHA-256 Internals Exploration

// Using sha2 crate: sha2 = "0.10"
use sha2::{Sha256, Digest};

fn main() {
    let message = b"abc";
    println!("Message: {}\n", String::from_utf8_lossy(message));

    // === DERIVE H FROM √PRIMES ===
    let primes = [2u32, 3, 5, 7, 11, 13, 17, 19];
    println!("=== H constants from √primes ===");
    for (i, &p) in primes.iter().enumerate() {
        let sqrt = (p as f64).sqrt();
        let frac = sqrt - sqrt.floor();
        let h = (frac * 0x100000000_f64) as u32;
        println!("H{} = frac(√{}) × 2³² = 0x{:08x}", i, p, h);
    }

    // === K FROM ∛PRIMES (first 4) ===
    println!("\n=== K constants from ∛primes ===");
    for (i, &p) in [2u32, 3, 5, 7].iter().enumerate() {
        let cbrt = (p as f64).cbrt();
        let frac = cbrt - cbrt.floor();
        let k = (frac * 0x100000000_f64) as u32;
        println!("K{} = frac(∛{}) × 2³² = 0x{:08x}", i, p, k);
    }

    // === USE STANDARD LIBRARY ===
    let mut hasher = Sha256::new();
    hasher.update(message);
    let result = hasher.finalize();
    println!("\nSHA-256 (sha2 crate): {:x}", result);

    let expected = "ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad";
    println!("Expected:             {}", expected);
    let result_hex = format!("{:x}", result);
    println!("Match: {}", if result_hex == expected { "✓" } else { "✗" });
}

🌊 Avalanche Effect

🎲 Collision Math

⟷ Symmetric Encryption

2,000 Years of Symmetric Ciphers

The limitation of symmetric encryption is key distribution: how do you and I agree on a shared secret key without an attacker intercepting it? This is the problem that asymmetric encryption solves — covered later.

🔢 Galois Fields

AES uses GF(2⁸) (Galois Field of 2⁸) for the MixColumns operation. To understand why, we need to understand what a field is.

A field is a mathematical structure where you can add, subtract, multiply, and divide (except by zero), and all operations follow familiar rules: addition and multiplication are commutative and associative, multiplication distributes over addition, and every non-zero element has a multiplicative inverse.

Examples of Fields:

• Real numbers (ℝ): You can add, subtract, multiply, and divide any real numbers. For any non-zero real number a, there's an inverse 1/a such that a × (1/a) = 1.
• GF(2) — the binary field: Just two elements: 0 and 1. Addition is XOR (0+0=0, 0+1=1, 1+1=0). Multiplication is AND (0×0=0, 0×1=0, 1×1=1). This is the simplest finite field.
• GF(2⁸) — the byte field: 256 elements (0 to 255). Addition is byte-wise XOR. Multiplication uses polynomial arithmetic modulo an irreducible polynomial (0x1b in AES). This is what AES uses.

Examples of Non-Fields:

• Integers (ℤ): You can add, subtract, and multiply, but you can't always divide. For example, 3 ÷ 2 = 1.5, which isn't an integer. Integers don't have multiplicative inverses (except 1 and -1).
• Natural numbers (ℕ): You can add and multiply, but you can't subtract (what's 2 - 5?) or divide (what's 3 ÷ 2?).
• Matrices: You can add and multiply matrices, but not all matrices have inverses, so division isn't always possible.

Why GF(2⁸) for AES? A Galois field is a finite field — it has a fixed, finite number of elements. GF(2⁸) has exactly 256 elements (0 to 255), which perfectly matches a byte. The "2⁸" means we're working with binary arithmetic (base 2) and polynomials of degree up to 8.

Multiplication in GF(2⁸) is different from regular multiplication. It uses XOR for addition and a special irreducible polynomial (0x1b, which represents x⁸ + x⁴ + x³ + x + 1) to handle overflow and keep results within the 256-element field. This provides diffusion — it mixes bits across bytes in a way that's mathematically reversible and efficient to compute. Each byte in a column affects all bytes in that column after MixColumns, spreading changes throughout the state. This is crucial for security: a single bit change in the plaintext should affect many bits in the ciphertext.

The multiply function in the AES implementation implements GF(2⁸) multiplication using bit shifts and XOR, with the irreducible polynomial 0x1b to keep results within the 256-element field.

🔐 AES — Advanced Encryption Standard

Block Cipher Modes

AES is a block cipher — it encrypts exactly 128 bits (16 bytes) at a time. But real messages are rarely exactly 128 bits. How do you encrypt a 1MB file? Block cipher modes define how to chain multiple blocks together securely.

ECB (Electronic Codebook) is the naive approach: encrypt each block independently with the same key. The problem? Identical plaintext blocks produce identical ciphertext blocks. Never use ECB.

Original

Encrypted with ECB

The famous "ECB penguin" — encrypting with ECB mode reveals the image structure because identical plaintext blocks (same-color regions) produce identical ciphertext blocks.

CBC (Cipher Block Chaining) fixes this by XORing each plaintext block with the previous ciphertext block before encryption. This creates a chain where each block depends on all previous blocks, hiding patterns. However, CBC doesn't detect tampering.

GCM (Galois/Counter Mode) is the modern standard. It uses counter mode (encrypting sequential counters, then XORing with plaintext) combined with a polynomial-based authentication tag. GCM provides both confidentiality and authenticity — attackers can't read or modify data undetected. Use GCM unless you have a specific reason not to.

1 SubBytes: Each byte is replaced using the S-Box lookup table. Provides non-linearity (confusion).

2 ShiftRows: Rows are circularly shifted left by 0, 1, 2, 3 positions. Spreads bytes across columns.

3 MixColumns: Each column is multiplied by a fixed matrix in GF(2⁸). Provides diffusion.

4 AddRoundKey: State is XORed with the round key. Introduces key material.

One round of AES encryption. Source: Wikipedia

JavaScript Python Go Rust

JavaScript — AES Implementation Run ▶

S-Box: Substitution Box

The S-Box is a lookup table that performs non-linear substitution. Each byte is replaced with another byte from a fixed table. This provides confusion — small input changes cause large, unpredictable output changes.

Rounds: 10/12/14

AES-128 uses 10 rounds, AES-192 uses 12, AES-256 uses 14. Each round applies all four operations (SubBytes, ShiftRows, MixColumns, AddRoundKey). More rounds = more security, but also more computation.

// AES-128 implementation (simplified educational version) // @info:rounds // AES operates on 16-byte (128-bit) blocks using 10 rounds // S-Box: non-linear substitution table (256 entries) const sBox = new Uint8Array([ 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 ]); function subBytes(state) { // @info:sbox // Replace each byte with S-Box lookup for (let i = 0; i < 16; i++) { state[i] = sBox[state[i]]; } } function shiftRows(state) { // Row 0: no shift // Row 1: circular left shift by 1 (rotate left) [state[1], state[5], state[9], state[13]] = [state[5], state[9], state[13], state[1]]; // Row 2: circular left shift by 2 (rotate left) [state[2], state[6], state[10], state[14]] = [state[10], state[14], state[2], state[6]]; // Row 3: circular left shift by 3 (rotate left) [state[3], state[7], state[11], state[15]] = [state[15], state[3], state[7], state[11]]; } function mixColumns(state) { // Galois field multiplication (simplified - full version uses GF(2^8) math) // This mixes bytes within each column for diffusion for (let c = 0; c < 4; c++) { const s0 = state[c * 4]; const s1 = state[c * 4 + 1]; const s2 = state[c * 4 + 2]; const s3 = state[c * 4 + 3]; state[c * 4] = multiply(0x02, s0) ^ multiply(0x03, s1) ^ s2 ^ s3; state[c * 4 + 1] = s0 ^ multiply(0x02, s1) ^ multiply(0x03, s2) ^ s3; state[c * 4 + 2] = s0 ^ s1 ^ multiply(0x02, s2) ^ multiply(0x03, s3); state[c * 4 + 3] = multiply(0x03, s0) ^ s1 ^ s2 ^ multiply(0x02, s3); } } function multiply(a, b) { // Galois field multiplication in GF(2^8) let result = 0; for (let i = 0; i < 8; i++) { if (b & 1) result ^= a; const hiBitSet = a & 0x80; a <<= 1; if (hiBitSet) a ^= 0x1b; // AES irreducible polynomial b >>= 1; } return result & 0xff; } function addRoundKey(state, roundKey) { // XOR state with round key for (let i = 0; i < 16; i++) { state[i] ^= roundKey[i]; } } // Simplified key expansion (full version is more complex) function expandKey(key) { const roundKeys = []; roundKeys.push(new Uint8Array(key)); // First round key = original key // Generate 10 more round keys (simplified - real AES uses Rcon) for (let round = 1; round <= 10; round++) { const prevKey = roundKeys[round - 1]; const newKey = new Uint8Array(16); // Simplified key expansion for (let i = 0; i < 16; i++) { newKey[i] = prevKey[i] ^ (round * 0x11 + i); } roundKeys.push(newKey); } return roundKeys; } function aesEncrypt(plaintext, key) { const state = new Uint8Array(plaintext); const roundKeys = expandKey(key); // Initial round: AddRoundKey only addRoundKey(state, roundKeys[0]); // 9 main rounds: SubBytes, ShiftRows, MixColumns, AddRoundKey for (let round = 1; round < 10; round++) { subBytes(state); shiftRows(state); mixColumns(state); addRoundKey(state, roundKeys[round]); } // Final round: SubBytes, ShiftRows, AddRoundKey (no MixColumns) subBytes(state); shiftRows(state); addRoundKey(state, roundKeys[10]); return state; } // Demo const key = new Uint8Array([0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c]); const plaintext = new TextEncoder().encode("Hello, AES! "); // Exactly 16 bytes console.log("=== AES-128 Encryption ==="); console.log("Plaintext:", Array.from(plaintext).map(b => '0x' + b.toString(16).padStart(2, '0')).join(' ')); console.log("Key:", Array.from(key).map(b => '0x' + b.toString(16).padStart(2, '0')).join(' ')); const ciphertext = aesEncrypt(plaintext, key); console.log("Ciphertext:", Array.from(ciphertext).map(b => '0x' + b.toString(16).padStart(2, '0')).join(' ')); console.log("\nNote: This is a simplified educational implementation."); console.log("Real AES uses proper key expansion (Rcon, RotWord, SubWord) and full GF(2^8) math.");

Output

Python — AES Implementation

# AES-128 implementation (simplified educational version)

# S-Box lookup table
S_BOX = bytes([
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
])

def sub_bytes(state):
    return bytes(S_BOX[b] for b in state)

def shift_rows(state):
    # Row 0: no shift
    # Row 1: circular left shift by 1 (rotate left)
    # Row 2: circular left shift by 2 (rotate left)
    # Row 3: circular left shift by 3 (rotate left)
    state = list(state)
    state[1], state[5], state[9], state[13] = state[5], state[9], state[13], state[1]
    state[2], state[6], state[10], state[14] = state[10], state[14], state[2], state[6]
    state[3], state[7], state[11], state[15] = state[15], state[3], state[7], state[11]
    return bytes(state)

def mix_columns(state):
    result = bytearray(16)
    for c in range(4):
        s0, s1, s2, s3 = state[c*4:(c+1)*4]
        result[c*4] = (2*s0 ^ 3*s1 ^ s2 ^ s3) & 0xff
        result[c*4+1] = (s0 ^ 2*s1 ^ 3*s2 ^ s3) & 0xff
        result[c*4+2] = (s0 ^ s1 ^ 2*s2 ^ 3*s3) & 0xff
        result[c*4+3] = (3*s0 ^ s1 ^ s2 ^ 2*s3) & 0xff
    return bytes(result)

def add_round_key(state, round_key):
    return bytes(a ^ b for a, b in zip(state, round_key))

def expand_key(key):
    round_keys = [key]
    for round_num in range(1, 11):
        prev_key = round_keys[-1]
        new_key = bytes(prev_key[i] ^ (round_num * 0x11 + i) for i in range(16))
        round_keys.append(new_key)
    return round_keys

def aes_encrypt(plaintext, key):
    state = bytearray(plaintext)
    round_keys = expand_key(key)
    
    state = add_round_key(state, round_keys[0])
    
    for round_num in range(1, 10):
        state = sub_bytes(state)
        state = shift_rows(state)
        state = mix_columns(state)
        state = add_round_key(state, round_keys[round_num])
    
    state = sub_bytes(state)
    state = shift_rows(state)
    state = add_round_key(state, round_keys[10])
    
    return bytes(state)

# Demo
key = bytes([0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6,
             0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c])
plaintext = b"Hello, AES!  "  # Exactly 16 bytes

print("=== AES-128 Encryption ===")
print("Plaintext:", ' '.join(f'0x{b:02x}' for b in plaintext))
print("Key:", ' '.join(f'0x{b:02x}' for b in key))

ciphertext = aes_encrypt(plaintext, key)
print("Ciphertext:", ' '.join(f'0x{b:02x}' for b in ciphertext))
print("\nNote: Simplified educational implementation.")

Go — AES Implementation

package main

import "fmt"

// S-Box lookup table
var sBox = [256]byte{
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16,
}

func subBytes(state []byte) {
    for i := range state {
        state[i] = sBox[state[i]]
    }
}

func shiftRows(state []byte) {
    // Row 0: no shift
    // Row 1: circular left shift by 1 (rotate left)
    // Row 2: circular left shift by 2 (rotate left)
    // Row 3: circular left shift by 3 (rotate left)
    state[1], state[5], state[9], state[13] = state[5], state[9], state[13], state[1]
    state[2], state[6], state[10], state[14] = state[10], state[14], state[2], state[6]
    state[3], state[7], state[11], state[15] = state[15], state[3], state[7], state[11]
}

func mixColumns(state []byte) {
    for c := 0; c < 4; c++ {
        s0, s1, s2, s3 := state[c*4], state[c*4+1], state[c*4+2], state[c*4+3]
        state[c*4] = (2*s0 ^ 3*s1 ^ s2 ^ s3) & 0xff
        state[c*4+1] = (s0 ^ 2*s1 ^ 3*s2 ^ s3) & 0xff
        state[c*4+2] = (s0 ^ s1 ^ 2*s2 ^ 3*s3) & 0xff
        state[c*4+3] = (3*s0 ^ s1 ^ s2 ^ 2*s3) & 0xff
    }
}

func addRoundKey(state, roundKey []byte) {
    for i := range state {
        state[i] ^= roundKey[i]
    }
}

func expandKey(key []byte) [][]byte {
    roundKeys := [][]byte{key}
    for round := 1; round <= 10; round++ {
        prevKey := roundKeys[round-1]
        newKey := make([]byte, 16)
        for i := range newKey {
            newKey[i] = prevKey[i] ^ byte(round*0x11+i)
        }
        roundKeys = append(roundKeys, newKey)
    }
    return roundKeys
}

func aesEncrypt(plaintext, key []byte) []byte {
    state := make([]byte, 16)
    copy(state, plaintext)
    roundKeys := expandKey(key)
    
    addRoundKey(state, roundKeys[0])
    
    for round := 1; round < 10; round++ {
        subBytes(state)
        shiftRows(state)
        mixColumns(state)
        addRoundKey(state, roundKeys[round])
    }
    
    subBytes(state)
    shiftRows(state)
    addRoundKey(state, roundKeys[10])
    
    return state
}

func main() {
    key := []byte{0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6,
                  0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c}
    plaintext := []byte("Hello, AES!  ")
    
    fmt.Println("=== AES-128 Encryption ===")
    fmt.Printf("Plaintext: ")
    for _, b := range plaintext {
        fmt.Printf("0x%02x ", b)
    }
    fmt.Println()
    
    ciphertext := aesEncrypt(plaintext, key)
    fmt.Printf("Ciphertext: ")
    for _, b := range ciphertext {
        fmt.Printf("0x%02x ", b)
    }
    fmt.Println("\n\nNote: Simplified educational implementation.")
}

Rust — AES Implementation

// AES-128 implementation (simplified educational version)

const S_BOX: [u8; 256] = [
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16,
];

fn sub_bytes(state: &mut [u8]) {
    for b in state.iter_mut() {
        *b = S_BOX[*b as usize];
    }
}

fn shift_rows(state: &mut [u8]) {
    // Row 0: no shift
    // Row 1: circular left shift by 1 (rotate left)
    // Row 2: circular left shift by 2 (rotate left)
    // Row 3: circular left shift by 3 (rotate left)
    state.swap(1, 5);
    state.swap(5, 9);
    state.swap(9, 13);
    state.swap(2, 10);
    state.swap(6, 14);
    state.swap(3, 15);
    state.swap(7, 3);
    state.swap(11, 7);
}

fn mix_columns(state: &mut [u8]) {
    for c in 0..4 {
        let s0 = state[c * 4];
        let s1 = state[c * 4 + 1];
        let s2 = state[c * 4 + 2];
        let s3 = state[c * 4 + 3];
        
        state[c * 4] = (2 * s0 ^ 3 * s1 ^ s2 ^ s3) & 0xff;
        state[c * 4 + 1] = (s0 ^ 2 * s1 ^ 3 * s2 ^ s3) & 0xff;
        state[c * 4 + 2] = (s0 ^ s1 ^ 2 * s2 ^ 3 * s3) & 0xff;
        state[c * 4 + 3] = (3 * s0 ^ s1 ^ s2 ^ 2 * s3) & 0xff;
    }
}

fn add_round_key(state: &mut [u8], round_key: &[u8]) {
    for i in 0..16 {
        state[i] ^= round_key[i];
    }
}

fn expand_key(key: &[u8]) -> Vec> {
    let mut round_keys = vec![key.to_vec()];
    for round in 1..=10 {
        let prev_key = &round_keys[round - 1];
        let new_key: Vec = (0..16)
            .map(|i| prev_key[i] ^ (round as u8 * 0x11 + i as u8))
            .collect();
        round_keys.push(new_key);
    }
    round_keys
}

fn aes_encrypt(plaintext: &[u8], key: &[u8]) -> Vec {
    let mut state = plaintext.to_vec();
    let round_keys = expand_key(key);
    
    add_round_key(&mut state, &round_keys[0]);
    
    for round in 1..10 {
        sub_bytes(&mut state);
        shift_rows(&mut state);
        mix_columns(&mut state);
        add_round_key(&mut state, &round_keys[round]);
    }
    
    sub_bytes(&mut state);
    shift_rows(&mut state);
    add_round_key(&mut state, &round_keys[10]);
    
    state
}

fn main() {
    let key = [0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6,
               0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c];
    let plaintext = b"Hello, AES!  ";
    
    println!("=== AES-128 Encryption ===");
    print!("Plaintext: ");
    for &b in plaintext.iter() {
        print!("0x{:02x} ", b);
    }
    println!();
    
    let ciphertext = aes_encrypt(plaintext, &key);
    print!("Ciphertext: ");
    for &b in ciphertext.iter() {
        print!("0x{:02x} ", b);
    }
    println!("\n\nNote: Simplified educational implementation.");
}

🔑 Keys & IVs

import os

print("=== Key & IV Generation ===\n")

# Generate keys
key_128 = os.urandom(16)  # 128 bits
key_256 = os.urandom(32)  # 256 bits
print(f"AES-128 key ({len(key_128)} bytes): {key_128.hex()[:32]}...")
print(f"AES-256 key ({len(key_256)} bytes): {key_256.hex()[:32]}...")

# Generate IV/Nonce
iv = os.urandom(12)  # 96-bit nonce for GCM
print(f"\nGCM nonce ({len(iv)} bytes): {iv.hex()}")

print("\n=== IV Rules ===")
print("• Must be UNIQUE per encryption (with same key)")
print("• Does NOT need to be secret")
print("• Store alongside ciphertext (prepend it)")
print("• 12 bytes (96 bits) for GCM")

print("\n=== Danger: IV Reuse ===")
print("Same (key, IV) pair used twice?")
print("Attacker gets: M1 ⊕ M2 = C1 ⊕ C2")
print("This leaks information about both messages!")

package main

import (
    "crypto/rand"
    "fmt"
)

func main() {
    fmt.Println("=== Key & IV Generation ===\n")

    // Generate keys
    key128 := make([]byte, 16) // 128 bits
    key256 := make([]byte, 32) // 256 bits
    rand.Read(key128)
    rand.Read(key256)
    fmt.Printf("AES-128 key: %x...\n", key128[:8])
    fmt.Printf("AES-256 key: %x...\n", key256[:8])

    // Generate nonce
    nonce := make([]byte, 12) // 96 bits for GCM
    rand.Read(nonce)
    fmt.Printf("\nGCM nonce: %x\n", nonce)

    fmt.Println("\n=== IV Rules ===")
    fmt.Println("• UNIQUE per encryption")
    fmt.Println("• NOT secret (store with ciphertext)")
    fmt.Println("• 12 bytes for AES-GCM")
}

use rand::RngCore;

fn main() {
    println!("=== Key & IV Generation ===\n");

    // Generate keys
    let mut key_128 = [0u8; 16];
    let mut key_256 = [0u8; 32];
    rand::thread_rng().fill_bytes(&mut key_128);
    rand::thread_rng().fill_bytes(&mut key_256);
    println!("AES-128 key: {:x?}...", &key_128[..8]);
    println!("AES-256 key: {:x?}...", &key_256[..8]);

    // Generate nonce
    let mut nonce = [0u8; 12]; // 96 bits for GCM
    rand::thread_rng().fill_bytes(&mut nonce);
    println!("\nGCM nonce: {:x?}", nonce);

    println!("\n=== IV Rules ===");
    println!("• UNIQUE per encryption");
    println!("• NOT secret");
    println!("• 12 bytes for AES-GCM");
}

⚿ Asymmetric Encryption

The Public-Key Revolution (1976-1978)

Before 1976, all cryptography was symmetric: both parties needed the same secret key. But how do you share a secret key with someone you've never met, over an insecure channel?

Diffie-Hellman (1976) — Whitfield Diffie and Martin Hellman published "New Directions in Cryptography," describing how two parties could agree on a shared secret over a public channel. This was considered impossible before — the mathematical insight was revolutionary.

RSA (1977) — Ron Rivest, Adi Shamir, and Leonard Adleman found a practical way to do public-key encryption and digital signatures. RSA was almost classified by the NSA and faced export restrictions as a "munition" until 1996.

How It Works

The magic: anything encrypted with the public key can only be decrypted with the corresponding private key. So if you want to send me a secret message, you encrypt it with my public key (which I've posted on my website), and even though an attacker can see the public key and the encrypted message, only I can decrypt it because only I have the private key.

This elegantly solves the key distribution problem. With symmetric encryption, we needed a secure channel to share the secret key — but if we had a secure channel, why would we need encryption? Asymmetric encryption lets us establish secure communication over an insecure channel. It's how HTTPS works: your browser encrypts a symmetric key using the server's public key, then both sides use that symmetric key for the actual communication.

The tradeoff is speed: RSA encryption is roughly 1000× slower than AES. That's why real systems use hybrid encryption — asymmetric crypto to exchange a symmetric key, then symmetric crypto for the actual data.

Asymmetric Algorithm Genealogy

🔢 RSA Math

# RSA key generation (simplified with small primes)
print("=== RSA Key Generation ===\n")

# Step 1: Choose two primes
p, q = 61, 53
print(f"Step 1: Primes p={p}, q={q}")

# Step 2: Compute n = p × q
n = p * q
print(f"Step 2: n = p×q = {n}")

# Step 3: Compute φ(n) = (p-1)(q-1)
phi_n = (p - 1) * (q - 1)
print(f"Step 3: φ(n) = {phi_n}")

# Step 4: Choose e (public exponent)
e = 17
print(f"Step 4: e = {e}")

# Step 5: Compute d = e⁻¹ mod φ(n)
d = pow(e, -1, phi_n)  # Python 3.8+
print(f"Step 5: d = {d}")

print(f"\nPublic key:  (n={n}, e={e})")
print(f"Private key: (n={n}, d={d})")

# Demo encryption
m = 42
c = pow(m, e, n)  # c = m^e mod n
m2 = pow(c, d, n)  # m = c^d mod n
print(f"\nEncrypt {m}: {c}")
print(f"Decrypt {c}: {m2}")

package main

import (
    "fmt"
    "math/big"
)

func main() {
    fmt.Println("=== RSA Key Generation ===\n")

    p := big.NewInt(61)
    q := big.NewInt(53)
    
    // n = p × q
    n := new(big.Int).Mul(p, q)
    fmt.Printf("n = p×q = %d\n", n)

    // φ(n) = (p-1)(q-1)
    pMinus1 := new(big.Int).Sub(p, big.NewInt(1))
    qMinus1 := new(big.Int).Sub(q, big.NewInt(1))
    phi := new(big.Int).Mul(pMinus1, qMinus1)
    fmt.Printf("φ(n) = %d\n", phi)

    e := big.NewInt(17)
    d := new(big.Int).ModInverse(e, phi)
    fmt.Printf("e = %d, d = %d\n", e, d)

    // Encrypt/decrypt
    m := big.NewInt(42)
    c := new(big.Int).Exp(m, e, n) // c = m^e mod n
    m2 := new(big.Int).Exp(c, d, n) // m = c^d mod n
    fmt.Printf("\nEncrypt %d → %d → %d\n", m, c, m2)
}

use num_bigint::BigUint;
use num_traits::One;

fn mod_inverse(a: &BigUint, m: &BigUint) -> BigUint {
    a.modpow(&(m - 2u32), m) // Only works when m is prime or coprime
}

fn main() {
    println!("=== RSA Key Generation ===\n");

    let p = BigUint::from(61u32);
    let q = BigUint::from(53u32);
    
    // n = p × q  
    let n = &p * &q;
    println!("n = p×q = {}", n);

    // φ(n) = (p-1)(q-1)
    let phi: BigUint = (&p - 1u32) * (&q - 1u32);
    println!("φ(n) = {}", phi);

    let e = BigUint::from(17u32);
    // d = e^(-1) mod φ(n) using extended Euclidean
    let d = BigUint::from(2753u32); // Precomputed for this example
    println!("e = {}, d = {}", e, d);

    // Encrypt/decrypt
    let m = BigUint::from(42u32);
    let c = m.modpow(&e, &n);
    let m2 = c.modpow(&d, &n);
    println!("\nEncrypt {} → {} → {}", m, c, m2);
}

🤝 Key Exchange

from cryptography.hazmat.primitives.asymmetric import x25519

# Generate key pairs
alice_private = x25519.X25519PrivateKey.generate()
alice_public = alice_private.public_key()

bob_private = x25519.X25519PrivateKey.generate()
bob_public = bob_private.public_key()

# Exchange public keys and derive shared secret
alice_shared = alice_private.exchange(bob_public)
bob_shared = bob_private.exchange(alice_public)

print("=== X25519 Key Exchange ===\n")
print(f"Alice public: {alice_public.public_bytes_raw().hex()[:32]}...")
print(f"Bob public:   {bob_public.public_bytes_raw().hex()[:32]}...")
print(f"\nAlice's shared secret: {alice_shared.hex()[:32]}...")
print(f"Bob's shared secret:   {bob_shared.hex()[:32]}...")
print(f"\nSecrets match: {alice_shared == bob_shared}")

package main

import (
    "crypto/rand"
    "fmt"
    "golang.org/x/crypto/curve25519"
)

func main() {
    // Generate Alice's key pair
    var alicePrivate, alicePublic [32]byte
    rand.Read(alicePrivate[:])
    curve25519.ScalarBaseMult(&alicePublic, &alicePrivate)

    // Generate Bob's key pair  
    var bobPrivate, bobPublic [32]byte
    rand.Read(bobPrivate[:])
    curve25519.ScalarBaseMult(&bobPublic, &bobPrivate)

    // Derive shared secrets
    var aliceShared, bobShared [32]byte
    curve25519.ScalarMult(&aliceShared, &alicePrivate, &bobPublic)
    curve25519.ScalarMult(&bobShared, &bobPrivate, &alicePublic)

    fmt.Println("=== X25519 Key Exchange ===\n")
    fmt.Printf("Alice shared: %x...\n", aliceShared[:16])
    fmt.Printf("Bob shared:   %x...\n", bobShared[:16])
    fmt.Printf("Match: %v\n", aliceShared == bobShared)
}

use x25519_dalek::{EphemeralSecret, PublicKey};
use rand::rngs::OsRng;

fn main() {
    // Generate Alice's key pair
    let alice_secret = EphemeralSecret::random_from_rng(OsRng);
    let alice_public = PublicKey::from(&alice_secret);

    // Generate Bob's key pair
    let bob_secret = EphemeralSecret::random_from_rng(OsRng);
    let bob_public = PublicKey::from(&bob_secret);

    // Derive shared secrets
    let alice_shared = alice_secret.diffie_hellman(&bob_public);
    let bob_shared = bob_secret.diffie_hellman(&alice_public);

    println!("=== X25519 Key Exchange ===\n");
    println!("Alice shared: {:x?}...", &alice_shared.as_bytes()[..16]);
    println!("Bob shared:   {:x?}...", &bob_shared.as_bytes()[..16]);
    println!("Match: {}", alice_shared.as_bytes() == bob_shared.as_bytes());
}

✓ Digital Signatures

🔍 Verification Flow

from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.primitives import hashes

# Generate key pair
private_key = rsa.generate_private_key(public_exponent=65537, key_size=2048)
public_key = private_key.public_key()

# Sign a message
message = b"Hello, World!"
signature = private_key.sign(
    message,
    padding.PSS(mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH),
    hashes.SHA256()
)
print(f"Message: {message}")
print(f"Signature: {signature.hex()[:40]}...")

# Verify (anyone can do this with public key)
try:
    public_key.verify(signature, message, 
        padding.PSS(mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH),
        hashes.SHA256())
    print("\n✓ Signature valid")
except:
    print("\n✗ Signature invalid")

package main

import (
    "crypto/rand"
    "crypto/rsa"
    "crypto/sha256"
    "fmt"
)

func main() {
    // Generate key pair
    privateKey, _ := rsa.GenerateKey(rand.Reader, 2048)
    publicKey := &privateKey.PublicKey

    message := []byte("Hello, World!")
    hash := sha256.Sum256(message)

    // Sign with private key
    signature, _ := rsa.SignPKCS1v15(rand.Reader, privateKey, 
        crypto.SHA256, hash[:])
    fmt.Printf("Message: %s\n", message)
    fmt.Printf("Signature: %x...\n", signature[:20])

    // Verify with public key
    err := rsa.VerifyPKCS1v15(publicKey, crypto.SHA256, hash[:], signature)
    if err == nil {
        fmt.Println("\n✓ Signature valid")
    } else {
        fmt.Println("\n✗ Signature invalid")
    }
}

use rsa::{RsaPrivateKey, RsaPublicKey, pkcs1v15::{SigningKey, VerifyingKey}};
use rsa::signature::{Signer, Verifier};
use sha2::Sha256;

fn main() {
    // Generate key pair
    let mut rng = rand::thread_rng();
    let private_key = RsaPrivateKey::new(&mut rng, 2048).unwrap();
    let public_key = RsaPublicKey::from(&private_key);

    let signing_key = SigningKey::::new(private_key);
    let verifying_key = VerifyingKey::::new(public_key);

    let message = b"Hello, World!";
    
    // Sign with private key
    let signature = signing_key.sign(message);
    println!("Message: {:?}", String::from_utf8_lossy(message));
    
    // Verify with public key
    match verifying_key.verify(message, &signature) {
        Ok(_) => println!("\n✓ Signature valid"),
        Err(_) => println!("\n✗ Signature invalid"),
    }
}

📜 Certificates & PKI

from cryptography import x509
from cryptography.x509.oid import NameOID
import ssl
import socket

# Fetch certificate from a real website
hostname = "google.com"
ctx = ssl.create_default_context()
with ctx.wrap_socket(socket.socket(), server_hostname=hostname) as s:
    s.connect((hostname, 443))
    cert_der = s.getpeercert(binary_form=True)

cert = x509.load_der_x509_certificate(cert_der)

print(f"=== Certificate for {hostname} ===\n")
print(f"Subject: {cert.subject.get_attributes_for_oid(NameOID.COMMON_NAME)[0].value}")
print(f"Issuer: {cert.issuer.get_attributes_for_oid(NameOID.ORGANIZATION_NAME)[0].value}")
print(f"Valid from: {cert.not_valid_before_utc}")
print(f"Valid until: {cert.not_valid_after_utc}")
print(f"Serial: {cert.serial_number}")
print(f"Signature algorithm: {cert.signature_algorithm_oid._name}")

package main

import (
    "crypto/tls"
    "fmt"
)

func main() {
    hostname := "google.com:443"
    conn, _ := tls.Dial("tcp", hostname, nil)
    defer conn.Close()

    cert := conn.ConnectionState().PeerCertificates[0]

    fmt.Println("=== Certificate for google.com ===\n")
    fmt.Printf("Subject: %s\n", cert.Subject.CommonName)
    fmt.Printf("Issuer: %s\n", cert.Issuer.Organization[0])
    fmt.Printf("Valid from: %s\n", cert.NotBefore)
    fmt.Printf("Valid until: %s\n", cert.NotAfter)
    fmt.Printf("Serial: %d\n", cert.SerialNumber)
    fmt.Printf("Signature algorithm: %s\n", cert.SignatureAlgorithm)
}

// Using rustls and x509-parser crates
use x509_parser::prelude::*;

fn main() {
    // In practice, you'd fetch cert bytes from TLS connection
    let cert_bytes: &[u8] = include_bytes!("cert.der");
    
    let (_, cert) = X509Certificate::from_der(cert_bytes).unwrap();
    
    println!("=== X.509 Certificate ===\n");
    println!("Subject: {:?}", cert.subject());
    println!("Issuer: {:?}", cert.issuer());
    println!("Valid from: {:?}", cert.validity().not_before);
    println!("Valid until: {:?}", cert.validity().not_after);
    println!("Serial: {:?}", cert.serial);
    println!("Signature algo: {:?}", cert.signature_algorithm.algorithm);
}

⊕ HMAC

HMAC (Hash-based Message Authentication Code) combines a secret key with a hash function. Unlike plain hashes, HMACs prove both integrity and authenticity — only someone with the secret key can create or verify the code. Used extensively in API authentication, session tokens, and secure cookies. The key difference from signatures: HMACs use symmetric keys (both parties share the secret), while signatures use asymmetric keys.

🔐 HMAC vs Plain Hash

Why not just concatenate the key and message, then hash? Because of length extension attacks! With SHA-256(key || message), an attacker who knows the hash can compute SHA-256(key || message || attacker_data) without knowing the key.

import hmac
import hashlib

key = b"supersecret"
message = b"Hello, World!"

# WRONG: hash(key + message) — vulnerable to length extension!
bad_mac = hashlib.sha256(key + message).hexdigest()
print("=== Don't do this ===")
print(f"SHA-256(key + msg): {bad_mac[:32]}...")
print("⚠️ Vulnerable to length extension attacks!\n")

# RIGHT: Use HMAC
good_mac = hmac.new(key, message, hashlib.sha256).hexdigest()
print("=== Do this ===")
print(f"HMAC-SHA256: {good_mac[:32]}...")
print("✓ Safe from length extension attacks")

print("\n=== Why HMAC works ===")
print("HMAC(K, M) = H((K⊕opad) || H((K⊕ipad) || M))")
print("Nested hashing prevents length extension")

package main

import (
    "crypto/hmac"
    "crypto/sha256"
    "fmt"
)

func main() {
    key := []byte("supersecret")
    message := []byte("Hello, World!")

    // WRONG: hash(key + message)
    h := sha256.New()
    h.Write(key)
    h.Write(message)
    badMac := h.Sum(nil)
    fmt.Printf("SHA-256(key+msg): %x...\n", badMac[:16])
    fmt.Println("⚠️ Vulnerable to length extension!\n")

    // RIGHT: Use HMAC
    mac := hmac.New(sha256.New, key)
    mac.Write(message)
    goodMac := mac.Sum(nil)
    fmt.Printf("HMAC-SHA256: %x...\n", goodMac[:16])
    fmt.Println("✓ Safe from length extension")
}

use hmac::{Hmac, Mac};
use sha2::Sha256;

type HmacSha256 = Hmac;

fn main() {
    let key = b"supersecret";
    let message = b"Hello, World!";

    // WRONG: Would be hash(key + message)
    // Don't do this — vulnerable to length extension!

    // RIGHT: Use HMAC
    let mut mac = HmacSha256::new_from_slice(key).unwrap();
    mac.update(message);
    let result = mac.finalize();
    
    println!("HMAC-SHA256: {:x?}...", &result.into_bytes()[..16]);
    println!("✓ Safe from length extension attacks");
    
    println!("\n=== Why HMAC works ===");
    println!("Nested structure: H((K⊕opad) || H((K⊕ipad) || M))");
}

⏱️ Timing Attacks

When comparing two strings, naive code stops at the first mismatch. An attacker can measure response times: if the first byte matches, it takes slightly longer. By trying all values for each position, they can extract the secret byte-by-byte.

import hmac
import secrets

secret = b"mysecretkey"
user_input = b"mysecretkey"

# WRONG: Early exit comparison
def bad_compare(a, b):
    if len(a) != len(b):
        return False
    for x, y in zip(a, b):
        if x != y:
            return False  # Exits early — timing leak!
    return True

# RIGHT: Constant-time comparison
def good_compare(a, b):
    return hmac.compare_digest(a, b)  # Always same time

print("=== Timing Attack Prevention ===\n")
print(f"bad_compare:  {bad_compare(secret, user_input)}")
print("⚠️ Vulnerable to timing attack\n")
print(f"hmac.compare_digest: {good_compare(secret, user_input)}")
print("✓ Constant time — safe from timing attacks")

print("\n=== Why this matters ===")
print("Attackers measure microsecond differences")
print("to extract secrets byte-by-byte")

package main

import (
    "crypto/subtle"
    "fmt"
)

func main() {
    secret := []byte("mysecretkey")
    userInput := []byte("mysecretkey")

    // WRONG: bytes.Equal exits early
    // badResult := bytes.Equal(secret, userInput)
    
    // RIGHT: constant-time comparison
    result := subtle.ConstantTimeCompare(secret, userInput)
    
    fmt.Println("=== Timing Attack Prevention ===\n")
    fmt.Printf("subtle.ConstantTimeCompare: %v\n", result == 1)
    fmt.Println("✓ Always takes same time")
    
    fmt.Println("\n=== The crypto/subtle package ===")
    fmt.Println("• ConstantTimeCompare — safe string comparison")
    fmt.Println("• ConstantTimeSelect — branchless selection")
    fmt.Println("• ConstantTimeCopy — conditional copy")
}

use subtle::ConstantTimeEq;

fn main() {
    let secret = b"mysecretkey";
    let user_input = b"mysecretkey";

    // WRONG: == operator exits early on mismatch
    // let bad = secret == user_input;
    
    // RIGHT: constant-time comparison with subtle crate
    let result = secret.ct_eq(user_input);
    
    println!("=== Timing Attack Prevention ===\n");
    println!("ct_eq result: {:?}", bool::from(result));
    println!("✓ Always takes same time");
    
    println!("\n=== The subtle crate ===");
    println!("• ct_eq — constant-time equality");
    println!("• conditional_select — branchless choice");
    println!("• Returns Choice type, not bool (prevents accidental use)");
}

◈ Key Derivation

Passwords make poor encryption keys — they're short and predictable. Key derivation functions like PBKDF2 stretch a password into a strong cryptographic key. The iteration count deliberately slows down the process, making brute-force attacks impractical. A unique salt prevents precomputed rainbow table attacks. Modern alternatives include Argon2 and scrypt, which also require significant memory.

🧂 Salt & Iterations

A salt is random data added to a password before hashing. It prevents attackers from using precomputed "rainbow tables." Iterations (or work factor) deliberately slow down hashing — making brute-force attacks take years instead of seconds.

import hashlib
import os

password = b"hunter2"
salt = os.urandom(16)  # Random 128-bit salt
iterations = 600_000   # OWASP 2023 recommendation

# PBKDF2 with salt and iterations
key = hashlib.pbkdf2_hmac('sha256', password, salt, iterations)

print("=== PBKDF2 with Salt & Iterations ===\n")
print(f"Password: {password.decode()}")
print(f"Salt: {salt.hex()}")
print(f"Iterations: {iterations:,}")
print(f"Derived key: {key.hex()[:32]}...")

print("\n=== Why this matters ===")
print("• Salt prevents rainbow tables")
print("• Iterations slow down brute force")
print("• 600k iterations ≈ 0.5-1 second per attempt")

package main

import (
    "crypto/rand"
    "crypto/sha256"
    "fmt"
    "golang.org/x/crypto/pbkdf2"
)

func main() {
    password := []byte("hunter2")
    salt := make([]byte, 16)
    rand.Read(salt)
    iterations := 600_000

    key := pbkdf2.Key(password, salt, iterations, 32, sha256.New)

    fmt.Println("=== PBKDF2 with Salt & Iterations ===\n")
    fmt.Printf("Password: %s\n", password)
    fmt.Printf("Salt: %x\n", salt)
    fmt.Printf("Iterations: %d\n", iterations)
    fmt.Printf("Key: %x...\n", key[:16])
}

use pbkdf2::pbkdf2_hmac;
use sha2::Sha256;
use rand::RngCore;

fn main() {
    let password = b"hunter2";
    let mut salt = [0u8; 16];
    rand::thread_rng().fill_bytes(&mut salt);
    let iterations = 600_000;
    
    let mut key = [0u8; 32];
    pbkdf2_hmac::(password, &salt, iterations, &mut key);

    println!("=== PBKDF2 with Salt & Iterations ===\n");
    println!("Password: {}", String::from_utf8_lossy(password));
    println!("Salt: {:x?}", salt);
    println!("Iterations: {}", iterations);
    println!("Key: {:x?}...", &key[..16]);
}

💾 Memory-Hard KDFs

PBKDF2 is CPU-bound — attackers can use GPUs (thousands of parallel cores) to crack passwords faster. Memory-hard functions like bcrypt, scrypt, and Argon2 require significant RAM, which is expensive on GPUs and ASICs.

import bcrypt
# pip install argon2-cffi
from argon2 import PasswordHasher

password = b"hunter2"

# bcrypt — classic memory-hard KDF
bcrypt_hash = bcrypt.hashpw(password, bcrypt.gensalt(rounds=12))
print("=== bcrypt ===")
print(f"Hash: {bcrypt_hash.decode()}")
print("✓ Memory-hard, GPU-resistant\n")

# Argon2id — modern winner (2015 PHC)
ph = PasswordHasher(time_cost=3, memory_cost=65536, parallelism=4)
argon2_hash = ph.hash(password.decode())
print("=== Argon2id ===")
print(f"Hash: {argon2_hash[:60]}...")
print("✓ Best choice for new applications")
print("  - time_cost: iterations")
print("  - memory_cost: KB of RAM (65MB here)")
print("  - parallelism: threads")

package main

import (
    "fmt"
    "golang.org/x/crypto/bcrypt"
    "golang.org/x/crypto/argon2"
    "crypto/rand"
)

func main() {
    password := []byte("hunter2")

    // bcrypt
    bcryptHash, _ := bcrypt.GenerateFromPassword(password, 12)
    fmt.Println("=== bcrypt ===")
    fmt.Printf("Hash: %s\n\n", bcryptHash)

    // Argon2id
    salt := make([]byte, 16)
    rand.Read(salt)
    argon2Hash := argon2.IDKey(password, salt, 3, 64*1024, 4, 32)
    
    fmt.Println("=== Argon2id ===")
    fmt.Printf("Hash: %x...\n", argon2Hash[:16])
    fmt.Println("Parameters: time=3, memory=64MB, threads=4")
}

use argon2::{Argon2, password_hash::{PasswordHasher, SaltString, rand_core::OsRng}};

fn main() {
    let password = b"hunter2";

    // Argon2id with recommended settings
    let salt = SaltString::generate(&mut OsRng);
    let argon2 = Argon2::default(); // Uses Argon2id
    
    let hash = argon2.hash_password(password, &salt).unwrap();
    
    println!("=== Argon2id ===");
    println!("Hash: {}...", &hash.to_string()[..60]);
    println!("\n✓ Memory-hard, GPU-resistant");
    println!("  Default: 19MB memory, 2 iterations, 1 thread");
}

⚄ Secure Random

Randomness is the foundation of all cryptography. Keys, IVs, salts, and nonces must be unpredictable. Standard random functions like Math.random() are pseudo-random — attackers can predict future values from past ones. Cryptographic random generators (CSPRNGs) use entropy from hardware sources (mouse movements, disk timing, CPU noise) to produce truly unpredictable values.

🎲 Entropy Sources

Entropy is randomness collected from physical sources. Your operating system continuously gathers entropy from unpredictable events: keyboard timing, mouse movements, disk I/O latency, network packet timing, and hardware noise. This "entropy pool" seeds the CSPRNG.

import os
import secrets

print("=== Entropy Sources ===\n")

# os.urandom — reads from /dev/urandom (Linux) or CryptGenRandom (Windows)
entropy = os.urandom(32)
print(f"os.urandom(32): {entropy.hex()[:32]}...")
print("→ Uses OS entropy pool (keyboard, mouse, disk I/O, etc.)\n")

# secrets module — Python 3.6+ recommended for crypto
token = secrets.token_hex(16)
print(f"secrets.token_hex(16): {token}")
print("→ Wrapper around os.urandom, recommended API\n")

# Check available entropy (Linux only)
try:
    with open('/proc/sys/kernel/random/entropy_avail', 'r') as f:
        available = f.read().strip()
        print(f"Entropy available: {available} bits")
except:
    print("Entropy check: N/A (not Linux)")

package main

import (
    "crypto/rand"
    "fmt"
    "io"
)

func main() {
    fmt.Println("=== Entropy Sources ===\n")

    // crypto/rand.Reader — reads from /dev/urandom
    entropy := make([]byte, 32)
    io.ReadFull(rand.Reader, entropy)
    fmt.Printf("crypto/rand: %x...\n", entropy[:16])
    fmt.Println("→ Uses OS entropy pool\n")

    // Generate random int
    var n [8]byte
    rand.Read(n[:])
    fmt.Printf("Random bytes: %x\n", n)
    
    fmt.Println("\n=== Go's crypto/rand ===")
    fmt.Println("• Always uses OS CSPRNG")
    fmt.Println("• Blocks if entropy is low (rare)")
    fmt.Println("• Safe for keys, IVs, tokens")
}

use rand::{RngCore, rngs::OsRng};
use getrandom::getrandom;

fn main() {
    println!("=== Entropy Sources ===\n");

    // OsRng — uses OS entropy directly
    let mut entropy = [0u8; 32];
    OsRng.fill_bytes(&mut entropy);
    println!("OsRng: {:x?}...", &entropy[..16]);
    println!("→ Uses OS entropy pool\n");

    // getrandom — lower-level OS interface
    let mut bytes = [0u8; 16];
    getrandom(&mut bytes).unwrap();
    println!("getrandom: {:x?}", bytes);
    
    println!("\n=== Rust's rand ecosystem ===");
    println!("• OsRng: OS-level CSPRNG");
    println!("• getrandom: System calls directly");
    println!("• thread_rng: Fast, seeded from OsRng");
}

🔀 PRNG vs CSPRNG

A PRNG (Pseudo-Random Number Generator) produces numbers that look random but are entirely determined by an initial seed. A CSPRNG (Cryptographically Secure PRNG) is designed so that even knowing previous outputs, you cannot predict future ones.

import random
import secrets

print("=== PRNG (random module) — NOT for crypto ===\n")
random.seed(12345)  # Predictable!
prng_nums = [random.randint(0, 100) for _ in range(5)]
print(f"random.seed(12345): {prng_nums}")
random.seed(12345)  # Same seed
prng_nums2 = [random.randint(0, 100) for _ in range(5)]
print(f"same seed again:    {prng_nums2}")
print("⚠️ Same seed = same sequence!\n")

print("=== CSPRNG (secrets module) — Use for crypto ===\n")
csprng_nums = [secrets.randbelow(100) for _ in range(5)]
print(f"secrets.randbelow: {csprng_nums}")
csprng_nums2 = [secrets.randbelow(100) for _ in range(5)]
print(f"secrets again:     {csprng_nums2}")
print("✓ Unpredictable every time!")

print("\n=== Quick guide ===")
print("• random: games, simulations, shuffling")
print("• secrets: tokens, keys, passwords")

package main

import (
    "crypto/rand"
    "fmt"
    "math/big"
    mrand "math/rand"
)

func main() {
    fmt.Println("=== PRNG (math/rand) — NOT for crypto ===\n")
    mrand.Seed(12345)
    nums := make([]int64, 5)
    for i := range nums { nums[i] = mrand.Int63n(100) }
    fmt.Printf("seed(12345): %v\n", nums)
    
    mrand.Seed(12345)
    for i := range nums { nums[i] = mrand.Int63n(100) }
    fmt.Printf("same seed:   %v\n", nums)
    fmt.Println("⚠️ Same seed = same sequence!\n")

    fmt.Println("=== CSPRNG (crypto/rand) — Use for crypto ===\n")
    for i := 0; i < 5; i++ {
        n, _ := rand.Int(rand.Reader, big.NewInt(100))
        fmt.Printf("crypto/rand: %d\n", n)
    }
    fmt.Println("✓ Unpredictable!")
}

use rand::{Rng, SeedableRng, rngs::{StdRng, OsRng}};

fn main() {
    println!("=== PRNG (seeded) — NOT for crypto ===\n");
    let mut prng = StdRng::seed_from_u64(12345);
    let nums: Vec = (0..5).map(|_| prng.gen_range(0..100)).collect();
    println!("seed(12345): {:?}", nums);
    
    let mut prng2 = StdRng::seed_from_u64(12345);
    let nums2: Vec = (0..5).map(|_| prng2.gen_range(0..100)).collect();
    println!("same seed:   {:?}", nums2);
    println!("⚠️ Same seed = same sequence!\n");

    println!("=== CSPRNG (OsRng) — Use for crypto ===\n");
    let mut csprng = OsRng;
    let secure: Vec = (0..5).map(|_| csprng.gen_range(0..100)).collect();
    println!("OsRng: {:?}", secure);
    println!("✓ Unpredictable!");
}

🔐 Password Security

Passwords are still the most common authentication method, and their storage is critical. Never store passwords in plaintext — use slow, salted hashing with algorithms designed for passwords. Modern attacks can test billions of hashes per second, so speed is the enemy of security.

🔑 Secure Remote Password (SRP)

What if you could prove you know a password without ever sending it? And what if the server never stored the password either — not even a hash? SRP (Secure Remote Password) is a PAKE (Password-Authenticated Key Exchange) protocol that achieves exactly this.

The Problem with Traditional Password Auth

Even with HTTPS and proper hashing, traditional password authentication has weaknesses:

• Password transmission — The password crosses the network (inside TLS, but still)
• Server storage — The server stores password hashes that could be stolen and cracked
• Phishing vulnerability — Users can be tricked into sending passwords to fake servers

What is PAKE?

Password-Authenticated Key Exchange (PAKE) protocols let two parties who share a password establish a secure session key, where:

• The password is never transmitted over the network
• Neither party learns anything useful if they don't already know the password
• An eavesdropper gains no information about the password
• Both parties can verify the other knows the password

SRP: Zero-Knowledge Password Proof

SRP provides mutual authentication — the client proves it knows the password to the server, AND the server proves it has the correct verifier (derived from the password) to the client. This prevents phishing: a fake server can't complete the protocol.

salt = random()
x = H(salt | password)      // Private key derived from password
v = g^x mod N               // Verifier (like a "public key" for the password)

Real-World Usage

SRP is used in production systems where password security is critical:

• Apple iCloud Keychain — Protects your password vault
• 1Password — Authenticates to the server without transmitting your master password
• ProtonMail — Secure email authentication
• AWS Cognito — Optional SRP-based authentication

🔄 SRP Protocol Flow

SRP authentication happens in two phases: registration (once) and authentication (each login). The math is based on Diffie-Hellman, but with password-derived values woven in.

Phase 1: Registration

When a user creates an account:

// Client-side (in browser or app)
salt = random(16 bytes)
x = H(salt | H(username | ":" | password))  // Private key
v = g^x mod N                                // Verifier

// Send to server: username, salt, v
// Server stores: {username, salt, v}
// Password and x NEVER leave the client

Phase 2: Authentication

When the user logs in, a challenge-response dance occurs:

// Client generates ephemeral key pair
a = random()                    // Client's private ephemeral
A = g^a mod N                   // Client's public ephemeral

// Client sends: username, A

// Server looks up user's salt and verifier v
// Server generates its own ephemeral key pair
b = random()                    // Server's private ephemeral
B = (k*v + g^b) mod N          // Server's public ephemeral (note: includes v!)

// Server sends: salt, B

// Both sides compute scrambling parameter
u = H(A | B)

// Client computes session key (using password-derived x)
x = H(salt | H(username | ":" | password))
S_client = (B - k * g^x) ^ (a + u*x) mod N
K_client = H(S_client)

// Server computes same session key (using stored verifier v)
S_server = (A * v^u) ^ b mod N
K_server = H(S_server)

// If password is correct: K_client == K_server

// Client proves it has K
M1 = H(A | B | K)
// Client sends M1

// Server verifies M1, then proves it has K
M2 = H(A | M1 | K)
// Server sends M2

// Client verifies M2
// Both now have verified shared secret K for the session

Why This Works

• Password never transmitted — Only derived values (A, B, M1, M2) cross the wire
• Verifier is useless alone — Attacker with v can't compute K without knowing the password
• Mutual authentication — Server must know v to compute K; fake server fails
• Forward secrecy — Ephemeral keys (a, b) mean past sessions stay safe
• Offline attack resistant — Eavesdropper can't brute-force without active participation

SRP vs Traditional Auth

Limitations

• Complexity — More implementation work than simple password hashing
• Round trips — Requires multiple exchanges (not stateless like JWT)
• Password strength still matters — Weak passwords can still be dictionary-attacked
• Not widely standardized — Different implementations may not interoperate

🍪 Sessions & Cookies

HTTP is stateless — each request is independent. Sessions maintain user state across requests using a session ID stored in a cookie. Session security is critical: session hijacking gives attackers full access to user accounts without knowing their password.

🎟️ JSON Web Tokens

JWTs are self-contained tokens that carry claims (data) and a signature. Unlike sessions, the server doesn't need to store state — it just verifies the signature. JWTs are used for API authentication, SSO, and stateless auth, but they come with tradeoffs around revocation and size.

📱 Multi-Factor Authentication

Passwords can be stolen, guessed, or phished. Multi-factor authentication (MFA) adds a second factor: something you have (phone, hardware key) or something you are (biometrics). TOTP (Time-based One-Time Password) is the most common — it generates 6-digit codes that change every 30 seconds.

🔑 OAuth 2.0

OAuth 2.0 is the standard for delegated authorization — letting apps access resources on behalf of users without sharing passwords. When you "Sign in with Google" or let an app access your calendar, that's OAuth. It separates who you are from what you can access.

🪪 OpenID Connect

OpenID Connect (OIDC) adds an identity layer on top of OAuth 2.0. While OAuth answers "what can this app access?", OIDC answers "who is this user?". It introduces the ID token — a JWT containing user identity claims — enabling single sign-on (SSO) and federated identity.

🔌 API Authentication

APIs need to verify who's calling them. Common methods include API keys (simple but limited), Bearer tokens (OAuth access tokens), and request signing (HMAC for integrity). The right choice depends on your security requirements and who consumes your API.

☁️ AWS Cognito

AWS Cognito is a managed identity service that handles user sign-up, sign-in, and access control. Instead of building authentication from scratch, you get OAuth 2.0, OpenID Connect, and SAML out of the box. Cognito issues standard JWTs with AWS-specific claims, integrates with social providers (Google, Facebook), and scales automatically.

🎫 Cognito Tokens

Cognito User Pools issue three types of tokens: ID tokens for user identity, Access tokens for API authorization, and Refresh tokens for getting new tokens. All are JWTs signed with RS256 using keys from the User Pool's JWKS endpoint.

🔌 Cognito Integration

There are multiple ways to integrate Cognito: the Hosted UI (AWS-managed login pages), Amplify (full SDK with UI components), or direct API calls (maximum control). Each has trade-offs between simplicity and customization.

🔒 TLS/HTTPS

TLS (Transport Layer Security) encrypts communication between browsers and servers. Without it, anyone on the network can read your passwords, cookies, and data. HTTPS is HTTP over TLS. Modern TLS 1.3 provides confidentiality, integrity, and authentication — the three pillars of secure communication.

🐳 Docker & Containers

What Containers Actually Are

A container is just a process with namespaces (isolated view of system resources) and cgroups (resource limits). There's no separate kernel — containers share the host's kernel, which is both their strength (lightweight, fast) and weakness (shared attack surface).

The Root Problem

By default, containers run as root. This is dangerous because:

• Root in container = root on host (same UID 0)
• Kernel exploits from container affect the host
• Misconfigured volumes can expose host filesystem
• Privileged containers have almost no isolation

Container Escape Vectors

"Container escape" means breaking out of the container's isolation to affect the host. Common vectors include:

Hardening Containers

Defense in depth for containers:

• Run as non-root: Use USER 1000 in Dockerfile or --user 1000:1000
• Drop capabilities: --cap-drop=ALL --cap-add=NET_BIND_SERVICE
• Read-only filesystem: --read-only with explicit tmpfs mounts
• No new privileges: --security-opt=no-new-privileges
• Seccomp profiles: Restrict available syscalls
• Rootless Docker: Run the Docker daemon itself as non-root

💉 Remote Code Injection

Injection Types

"Injection" happens when untrusted data gets interpreted as code. Different contexts lead to different injection types:

Command Injection

Happens when user input is passed to shell commands. Attackers use shell metacharacters to escape the intended command:

Shell metacharacters that enable injection:

• ; — command separator
• | — pipe output to another command
• && and || — conditional execution
• `cmd` or $(cmd) — command substitution
• > and >> — redirect output to file

The eval() Trap

eval() executes strings as code. It's almost never needed and always dangerous with user input:

Server-Side Template Injection (SSTI)

Template engines like Jinja2, Twig, and Freemarker execute template syntax. If user input is rendered as a template (not just data), attackers can execute code:

Deserialization Attacks

Serialization converts objects to bytes for storage or transmission. Deserializing untrusted data can execute code during object reconstruction:

Defense Principles

• Never trust user input — validate, sanitize, and escape appropriately for context
• Avoid dangerous functions — eval(), exec(), system(), shell_exec(), unserialize()
• Use parameterized APIs — prepared statements for SQL, arrays for subprocess
• Principle of least privilege — run apps as non-root with minimal permissions
• Sandbox execution — containers, VMs, or restricted interpreters for untrusted code
• Web Application Firewalls — detect and block common injection patterns

📜 Cross-Site Scripting (XSS)

The Three Types

XSS is categorized by how the malicious script reaches the victim's browser:

Reflected XSS

The attacker crafts a URL containing a script. When the victim clicks it, the server includes the script in its response:

The victim sees a legitimate-looking link to your site. When they click it, their browser executes the attacker's script in your site's context — with access to cookies, localStorage, and the ability to make authenticated requests.

Stored XSS

More dangerous because it doesn't require tricking users into clicking links. The script is saved permanently:

DOM-based XSS

The server never sees the payload — it's entirely client-side. Vulnerable when JavaScript reads from untrusted sources and writes to dangerous sinks:

Dangerous sources: location.hash, location.search, document.referrer, postMessage data

Dangerous sinks: innerHTML, document.write(), eval(), setTimeout(string)

Defense: Context-Aware Escaping

The fix depends on where untrusted data appears:

Defense: Content Security Policy

CSP is a defense-in-depth header that restricts what scripts can run. Even if XSS gets through, CSP can block it:

This allows only scripts from your domain — inline scripts and eval() are blocked. We'll cover CSP in detail in the Security Headers section.

🎭 Cross-Site Request Forgery (CSRF)

How CSRF Works

When you visit a site, your browser automatically sends that site's cookies with every request — even if the request originates from a different site:

If the victim is logged into bank.com and visits evil.com, their browser makes an authenticated request to bank.com. The bank sees a valid session cookie and processes the transfer.

What's Vulnerable

CSRF only works against state-changing operations that rely solely on cookies for authentication:

• Changing email/password
• Making purchases or transfers
• Posting content
• Changing settings
• Admin actions

Safe from CSRF: GET requests (should be read-only anyway), APIs using Authorization headers (not cookies), and requests requiring data the attacker can't know.

Defense: CSRF Tokens

Include a secret token in forms that the attacker can't know or guess:

The attacker can make the victim's browser send cookies, but can't read the CSRF token from your page (same-origin policy prevents this). Without the token, the request is rejected.

Defense: SameSite Cookies

Modern browsers support the SameSite cookie attribute, which prevents cookies from being sent on cross-site requests:

Defense: Custom Headers

For AJAX requests, require a custom header that simple cross-origin requests can't include:

Cross-origin requests can't set custom headers without CORS preflight approval. Since you control your CORS policy, attackers can't add these headers from their site.

🛡️ Security Headers

Content-Security-Policy (CSP)

CSP controls what resources can load and execute on your page. It's the most powerful security header:

Strict-Transport-Security (HSTS)

Forces browsers to only use HTTPS for your site, preventing SSL stripping attacks:

• max-age — How long to remember (seconds). 31536000 = 1 year
• includeSubDomains — Apply to all subdomains
• preload — Submit to browser preload lists (permanent!)

X-Frame-Options / frame-ancestors

Prevents your page from being embedded in iframes, stopping clickjacking attacks:

Clickjacking: Attacker overlays your page (invisible iframe) on their page. When users think they're clicking the attacker's button, they're actually clicking yours — liking posts, following accounts, or clicking "delete account."

Other Important Headers

A Complete Security Headers Set

Test your headers at securityheaders.com — it grades your site and explains each missing header.

🌐 Cross-Origin Resource Sharing (CORS)

The Same-Origin Policy

The browser's Same-Origin Policy (SOP) is the foundation. An "origin" is the combination of scheme + host + port:

Without the Same-Origin Policy, any website could read your bank balance, access your email, or steal session tokens from other sites you're logged into. SOP is the browser's primary defense against malicious websites.

When You Need CORS

CORS is needed when your frontend (running on one origin) needs to make API calls to a backend (on a different origin):

Simple Requests vs Preflight

Browsers classify requests into two categories:

Simple requests (no preflight) meet ALL of these conditions:

• Method is GET, HEAD, or POST
• Only "simple" headers: Accept, Accept-Language, Content-Language, Content-Type
• Content-Type is only: text/plain, multipart/form-data, or application/x-www-form-urlencoded

Preflighted requests — anything else. Before the actual request, the browser sends an OPTIONS request asking "is this allowed?"

CORS Response Headers

Common CORS Configurations

Server-Side Implementation

Debugging CORS Errors

CORS errors in the browser console can be cryptic. Here's how to diagnose them:

CORS Security Pitfalls

CORS vs CSRF

CORS and CSRF protection are related but different:

• CORS prevents JavaScript from reading cross-origin responses
• CSRF tokens prevent unauthorized state-changing requests

CORS doesn't block all cross-origin requests — only reading responses. A malicious site can still trigger a POST to your server; CORS just prevents it from seeing the response. That's why you need CSRF protection for state-changing operations.

🔒 Content Security Policy (CSP)

How CSP Works

CSP is delivered as an HTTP response header. When the browser sees this header, it enforces the policy for that page:

CSP Directives

Each directive controls a different type of resource:

Source Values

Nonces and Hashes

Instead of allowing all inline scripts ('unsafe-inline'), you can allow specific scripts using nonces or hashes:

Strict CSP (Recommended)

Modern CSP best practice uses nonces or hashes instead of URL allowlists, because allowlists often include CDNs that host attacker-controllable content (JSONP endpoints, old library versions):

Report-Only Mode

Deploy CSP safely by testing in report-only mode first:

Common CSP Mistakes

CSP for Single-Page Apps

SPAs often need special handling for bundled JavaScript and dynamic styles:

Server Implementation

⚛ Post-Quantum Cryptography

The Quantum Threat

What breaks: RSA, ECDSA, ECDH, Ed25519 — anything based on factoring or discrete logarithms. A quantum computer with enough qubits could break 2048-bit RSA in hours.

What survives: Symmetric encryption (AES) and hashing (SHA-256) are weakened but not broken. Grover's algorithm halves key strength — AES-256 becomes ~128-bit security, still safe. SHA-256 remains collision-resistant.

New Standards (2024)

NIST ran another open competition (2016-2024), like they did for AES. The winners use mathematical problems believed to be hard even for quantum computers:

Trust & Backdoors

The Snowden revelations (2013) showed the NSA had been working to undermine cryptographic standards. The most damning: Dual_EC_DRBG, a random number generator standardized by NIST, contained a suspected backdoor. The NSA had paid RSA Security $10 million to make it the default in their products.